対数正規分布

対数正規分布

確率密度関数 μ=0
累積分布関数 μ=0
母数	[math]\mu \in \mathbb{R} [/math] [math]\sigma \gt 0\,[/math]
台	[math]x\in (0,\infty)[/math]
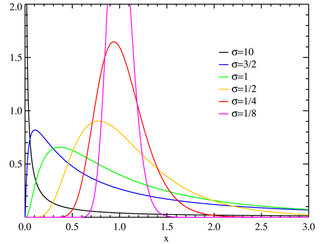
テンプレート:確率分布/リンク 密度	[math] f(x) = \frac{1}{\sqrt{2\pi} \sigma x} \exp \left( -\frac{ (\ln{x}-\mu)^2}{2\sigma^2} \right)[/math]
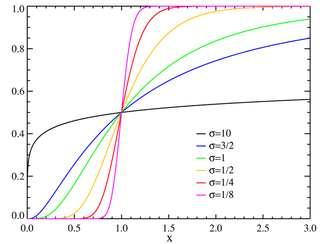
累積分布関数	[math]\frac{1}{2} \operatorname{erfc}\!\left[-\frac{\ln{x} - \mu}{\sqrt{2}\sigma}\right][/math]
期待値	[math]e^{\mu + {\sigma^2 }/{2} } [/math]
中央値	[math]e^{\mu}[/math]
最頻値	[math] e^{\mu-\sigma^2}[/math]
分散	[math] e^{2\mu+\sigma^2}(e^{\sigma^2}-1)[/math]
歪度	[math] \sqrt{e^{\sigma^2}-1}(e^{\sigma^2}+2)[/math]
尖度	[math] e^{4\sigma^2}+2e^{3\sigma^2}+3e^{2\sigma^2}-6 \,[/math]
エントロピー	[math]\frac{1}{2} + \frac{1}{2} \ln{(2\pi\sigma^2)} + \mu [/math]

対数正規分布（たいすうせいきぶんぷ、英: log-normal distribution）

ジブラ分布ともいう。確率分布の一種で，この分布に従う確率変数の対数が正規分布に従うことから名づけられたもの。一般に右に裾の広がった形をしており，家計間の所得分布などによくあてはまる。

---

楽天市場検索:

---