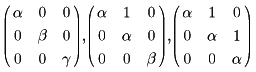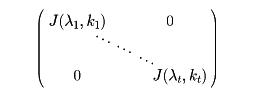「ジョルダン標準形」の版間の差分

提供: miniwiki
移動先:案内、検索
(→‎線形変換)
 
細
 
(同じ利用者による、間の2版が非表示)
1行目: 1行目:
−
'''ジョルダン標準形'''（ジョルダンひょうじゅんけい、{{lang-en-short|Jordan normal form}}）とは、[[代数的閉体]]（例えば[[複素数]][[可換体|体]]）上の[[正方行列]]に対する標準形のことである。任意の正方行列は本質的にただ一つのジョルダン標準形と[[行列の相似|相似]]である。名前は[[カミーユ・ジョルダン]]にちなむ。
+
'''ジョルダン標準形'''（ジョルダンひょうじゅんけい、{{lang-en-short|Jordan normal form}}）
  
−
== 定義 ==
+
逆行列の存在する行列を正則行列という。正方行列<i>A</i>を正則行列<i>P</i>を用いて変換する（<i>P</i><sup>-1</sup><i>AP</i>を求める）とき、いちばん簡潔に求められる方法はフランスの数学者ジョルダンがみいだしたジョルダンの標準形である。たとえば三次正方行列は次のいずれかの形にかならず変換される。
−
=== 行列 ===
 
−
[[代数的閉体]] {{mvar|K}} 成分の {{mvar|n}} 次[[正方行列]]
 
−
:<math>J_n(\lambda) =
 
−
\begin{pmatrix}
 
−
\lambda &    1    &        &        &    0    \\
 
−
        & \lambda &  1    &        &        \\
 
−
        &        & \ddots & \ddots  &        \\
 
−
        &        &        & \lambda &    1    \\
 
−
  0    &        &        &        & \lambda \\
 
−
\end{pmatrix}
 
−
</math>
 
−
を'''ジョルダン細胞'''という{{Sfn|斎藤|1966|p=187}}。
 
−
任意の正方行列 {{mvar|M}} に対して
 
−
:<math> PMP^{-1} = \begin{pmatrix}
 
−
J_{n_1}(\lambda_1) &        &        0          \\
 
−
                  & \ddots &                    \\
 
−
        0          &        & J_{n_k}(\lambda_k) \\
 
−
\end{pmatrix}
 
−
</math>
 
−
となる[[正則行列]] {{mvar|P}} が存在する{{Sfn|斎藤|1966|loc=第6章 定理[2.2]}}。
 
−
このとき {{math|''&lambda;''<sub>''i''</sub>}} は {{mvar|M}} の[[固有値]]である。
 
−
この行列 {{math|''PMP''<sup>&minus;1</sup>}} のことを行列 {{mvar|M}} の'''ジョルダン標準形'''という{{Sfn|斎藤|1966|p=191}}。
 
  
−
=== 線形変換 ===
+
[[ファイル:00121081000100.gif|フレームなし]]
−
[[代数的閉体]] {{mvar|K}} 上の[[ベクトル空間の次元|有限次元]][[線形空間]]を {{mvar|V}} とし、[[線形変換]] {{math|''&fnof;'' : ''V'' &rarr; ''V''}} をとる。
 
−
{{mvar|&fnof;}} が'''半単純'''（semisimple）であるとは、線形空間 {{mvar|V}} が <math> V = \bigoplus V_\lambda </math> と {{mvar|&fnof;}} の[[固有値]] {{math|''&lambda;'' &isin; ''K''}} の[[固有空間]] {{math|''V''<sub>''&lambda;''</sub> {{=}} { ''v'' &isin; ''V'' {{!}} ''&fnof;''(''v'') {{=}} ''&lambda;v'' } }}の[[ベクトル空間の直和|直和]]として表せることである。
 
−
また {{mvar|&fnof;}} が '''冪零'''（nilpotent） であるとは、ある[[自然数]] {{mvar|r}} が存在して {{math|''f<sup>r</sup>'' {{=}} 0}} となることである。
 
  
−
任意の線形変換 {{math|''&fnof;'' : ''V'' &rarr; ''V''}} に対して、半単純線形変換 {{math|''&fnof;''<sub>s</sub>}} と冪零線形変換 {{math|''&fnof;''<sub>n</sub>}} で
+
ただし、α、β、γはかならずしも相異なるとは限らない複素数（実数でもよい）である。
−
:<math> f = f_{\rm s} + f_{\rm n}, \quad f_\mathrm{s} f_\mathrm{n} - f_\mathrm{n} f_\mathrm{s} = 0 </math>
 
−
を満たすものが一意的に存在する。このとき {{math|''&fnof;'' {{=}} ''&fnof;''<sub>s</sub> + ''&fnof;''<sub>n</sub>}} のことを（加法的）'''ジョルダン分解'''といい、
 
−
{{math|''&fnof;''<sub>s</sub>}} を {{mvar|&fnof;}} の'''半単純成分'''、{{math|''&fnof;''<sub>n</sub>}} を {{mvar|&fnof;}} の'''冪零成分'''という。
 
  
−
線形空間 {{mvar|V}} の[[基底 (線型代数学)|基底]] <math>\{\, e_{ij} \mid i=1, \dotsc ,k;~j=1, \dotsc ,n_i \,\}</math> が線形変換 {{mvar|&fnof;}} の'''ジョルダン基底''' であるとは、{{math|''e''<sub>''i''0</sub> {{=}} 0}} とおいたとき
+
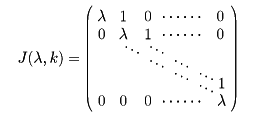
　一般的にいうと、まず、λを複素数（実数でもよい）とするとき、<i>k</i>次の行列J(λ, <i>k</i>)を
−
:<math> f( e_{ij} )= \lambda_i e_{ij} + e_{i(j-1)} </math>
 
−
が基底の任意の元 {{math|''e''<sub>''ij''</sub>}} について成り立つことである。
 
−
ジョルダン基底に関する {{mvar|&fnof;}} の表現行列がジョルダン標準形である。
 
  
−
== 例 ==
+
[[ファイル:00121081000200.gif|フレームなし]]
−
対角行列は次数が1のジョルダン細胞のみからなるジョルダン標準形である。
 
  
−
次の[[複素数|複素]]成分正方行列 {{mvar|M}} のジョルダン標準形は次のようになる。
+
により定義する。いくつかの<i>J</i>(λ, <i>k</i>)の形の行列を対角形に並べた行列
−
:<math>  
 
−
M = \begin{pmatrix} 1 & 2 \\ -2 & 5 \end{pmatrix},~
 
−
P = \begin{pmatrix} 0 & 1 \\ -2 & 2 \end{pmatrix},~
 
−
PMP^{-1} = \begin{pmatrix} 3 & 1 \\ 0 & 3 \end{pmatrix}
 
−
</math>
 
−
また次で定めるベクトル {{mvar|u}}, {{mvar|v}} は {{math|''Mu'' {{=}} 3''u''}} と {{math|''Mv'' {{=}} 3''v'' + ''u''}} とを満たすので行列 {{mvar|M}} のジョルダン基底である。
 
−
:<math>  
 
−
u = \begin{pmatrix} 1 \\ 1 \end{pmatrix},~
 
−
v = \begin{pmatrix} -1/2 \\ 0 \end{pmatrix}
 
−
</math>
 
  
−
この行列 {{mvar|M}} の半単純成分 {{mvar|S}} と冪零成分 {{mvar|N}} への分解は次のようになる。
+
[[ファイル:00121081000300.gif|フレームなし]]
−
:<math>
 
−
S = \begin{pmatrix} 3 & \\ & 3 \end{pmatrix},~
 
−
N = \begin{pmatrix} -2 & 2 \\ -2 & 2 \end{pmatrix}, ~
 
−
M = S + N
 
−
</math>
 
−
この分解は {{math|''N''<sup>2</sup> {{=}} 0}} や {{math|''SN'' {{=}} ''NS''}} が成り立つので、
 
−
[[行列の指数関数]]や[[冪乗]]の計算に役立つ。
 
−
:<math>
 
−
e^{Mt} = e^{St + Nt} = e^{St}e^{Nt} = e^{St}(I + Nt) = e^{3t}\begin{pmatrix} 1 - 2t & 2t \\ -2t & 1 + 2t \end{pmatrix}
 
−
</math>
 
−
:<math>
 
−
M^n = (S + N)^n = S^n + nS^{n - 1}N =
 
−
3^{n - 1}\begin{pmatrix} 3 - 2n & 2n \\ -2n & 3 + 2n \end{pmatrix}
 
−
</math>
 
  
−
== アルゴリズム ==
+
をジョルダン行列という。<i>A</i>を正方行列とすれば<i>P</i><sup>-1</sup><i>AP</i>がジョルダン行列となる正則行列<i>P</i>がかならず存在する。<i>A</i>のジョルダン行列は<i>A</i>によって一意的に定まる。
−
{{mvar|n}} 次[[正方行列]] {{mvar|A}}のジョルダン標準形は次のように計算できる{{sfn|Hogben|2007|loc={{google books quote|id=kATOBQAAQBAJ|page=SA6-PA5|6-5}}}}。以下では {{mvar|I}} で {{mvar|n}} 次[[単位行列]]を表す。
 
  
−
;入力
+
{{テンプレート:20180815sk}}
−
:{{mvar|n}} 次正方行列 {{mvar|A}}
 
−
;出力
 
−
:{{math|''P''<sup>&minus;1</sup>''AP''}} がジョルダン標準形となる {{mvar|n}} 次[[正則行列]] {{mvar|P}}
 
−
;アルゴリズム
 
−
# 行列 {{mvar|A}} の相異なる[[固有値]] {{math|''&lambda;''<sub>1</sub>, &hellip;, ''&lambda;''<sub>''s''</sub>}} を求める
 
−
# {{math|''A<sub>i</sub>'' {{=}} ''A'' &minus; ''&lambda;<sub>i</sub> I''}} とおく
 
−
# {{math|[[行列の階数|rank]] ''A<sub>i</sub> <sup>k<sub>i</sub></sup>'' {{=}} rank ''A<sub>i</sub>'' <sup>''k<sub>i</sub>''+1</sup>}} となる最小の自然数 {{mvar|k<sub>i</sub>}} を求める
 
−
# {{math|''W<sub>i,j</sub>'' {{=}} [[線型写像#核・像と全射性・単射性|im]] ''A<sub>i</sub> <sup>j</sup>'' &cap; [[線型写像#核・像と全射性・単射性|ker]] ''A<sub>i</sub>''}} とおく
 
−
# 部分空間の増大列 {{math|''W''<sub>''i,k<sub>i</sub>''&minus;1</sub> &sub; &hellip; &sub; ''W''<sub>''i'',1</sub> &sub; ''W''<sub>''i'',0</sub> {{=}} ker ''A<sub>i</sub>''}} に沿って {{math|ker ''A<sub>i</sub>''}} の[[ハメル基底|基底]] {{math|''b''<sub>''i'',1</sub>, &hellip;, ''b<sub>i,t<sub>i</sub></sub>''}} を求める<ref>つまり {{math|1 &le; ''d''<sub>1</sub> &le; ''d''<sub>2</sub> &le; &hellip; &le; ''t<sub>i</sub>''}} があって、{{math|''W''<sub>''i'',''k<sub>i</sub>''&minus;1</sub> {{=}} &lang; ''b''<sub>''i'',1</sub>, &hellip;, ''b''<sub>''i'',''d''<sub>1</sub></sub> &rang;}}, {{math|''W''<sub>''i'',''k<sub>i</sub>''&minus;2</sub> {{=}} &lang; ''b''<sub>''i'',1</sub>, &hellip;, ''b''<sub>''i'',''d''<sub>2</sub></sub> &rang;}}, &hellip;, {{math|''W''<sub>''i'',0</sub> {{=}} &lang; ''b''<sub>''i'',1</sub>, &hellip;, ''b''<sub>''i,t<sub>i</sub></sub>'' &rang;}}となるように基底をとる</ref>
 
−
# {{math|''b<sub>i,j</sub>'' &isin; ''W<sub>i,d<sub>i,j</sub></sub>'' [[差集合|&minus;]] ''W''<sub>''i'',''d<sub>i,j</sub>''+1</sub>}} となる自然数 {{mvar|d<sub>i,j</sub>}} を求める
 
−
# [[連立一次方程式]] {{math| ''A<sub>i</sub>'' <sup>''d<sub>i,j</sub>''</sup> ''x<sub>i,j</sub>'' {{=}} ''b<sub>i,j</sub>''}} の解 {{mvar|x<sub>i,j</sub>}} を求める
 
−
# {{math|''e<sub>i,j</sub>'' {{=}} ''A<sub>i</sub>'' <sup>''j''</sup> ''x<sub>i,j</sub>''}} とおく
 
−
# {{math|''P<sub>i,j</sub>'' {{=}} [''e''<sub>''i'',''d<sub>i,j</sub>''</sub>, &hellip;, ''e''<sub>''i'',1</sub>, ''e''<sub>''i'',0</sub>]}} とおく
 
−
# {{math|''P'' {{=}} [''P''<sub>1,1</sub>, &hellip;, ''P''<sub>1,''t''<sub>1</sub></sub>, &hellip;, ''P''<sub>''s'',1</sub>, &hellip;, ''P''<sub>''s,t<sub>s</sub>''</sub>]}} を出力
 
−
 
 
−
== 標準形の存在証明 ==
 
−
;定理:　任意の線形変換 <math>f</math> に対しジョルダン基底は存在する。
 
−
 
 
−
証明は線形空間の次元 <math>n=\dim V</math> についての帰納法で、<math>n=1</math> ならすべての基底がジョルダン基底だからOK、
 
−
<math>n-1</math> までOKとして、 <math>n=\dim V</math> とする。次の明らかな補題が証明の鍵である。
 
−
 
 
−
;補題:　<math>\{ e_{ij} \}</math> が <math>f</math> のジョルダン基底なら、<math> f-\lambda 1_V</math> のジョルダン基底でもある。ここで <math>\lambda</math> は任意のスカラー。
 
−
 
 
−
この補題により <math>\operatorname{rank} f=r <n </math> の場合に示せばよい。
 
−
このとき <math>V'=\operatorname{im} f,\ f'=f|_{V'}</math> とすると、帰納法の仮定で、
 
−
<math>f'</math> のジョルダン基底 <math>\{e_{ij} \} </math> がとれる。
 
−
番号を <math>\lambda_1=\lambda_2=\dotsb =\lambda_s=0 </math>、<math>i>s </math> なら <math>\lambda_i \neq 0</math> となるようにとる。<math> e_{11},e_{21},\dotsc,e_{s1}</math> は <math>\ker f </math> の元で線形独立だから、これらに <math>b_1,b_2,\dotsc,b_{n-r-s} </math> を加えて <math>\ker f </math> の基底を作る。また <math>V</math> の元 <math>c_1,c_2,\dotsc,c_s</math> を <math>f(c_i)=e_{i n_i }</math> となるようにとる。このとき <math>n</math> 個のベクトル
 
−
<math>\{ e_{ij} \} \cup \{ b_i\}\cup \{ c_i \}</math> が線形独立であることは容易にわかり、
 
−
これらは <math>V</math> の基底である。<math>c_i =e_{i n_i +1},\ b_i =e_{k+i 1}</math> と番号づけると、これが <math>f</math> のジョルダン基底となる。[証明終わり]
 
−
 
 
−
<math>V=K^n</math> で <math>f</math> が行列 <math>A=(a_1,a_2,\dotsc,a_n)</math> で表されるとき、 <math>\operatorname{rank}A=r</math> なら、 <math>a_1,a_2,\dotsc,a_r</math> が線形独立としてよい。このとき
 
−
<math> A=\begin{pmatrix}  {A_{11}}  &  {A_{12}}  \\ {A_{21}}  &  {A_{22}}  \end{pmatrix} </math> は行変形で
 
−
<math>\begin{pmatrix}  {E_r}  &  R \\ 0  &  0  \end{pmatrix}</math> と簡約化される。
 
−
 
 
−
;命題:　上のとき、 <math>a_1,a_2,\dotsc,a_r</math> は <math>V'</math> の基底であるが、この基底に関する <math>f'</math> の表現行列は <math> A_{11}+R A_{21} </math> である。
 
−
 
 
−
命題の証明は略するが、これを用いると上のジョルダン基底の存在証明は、同時に行列のジョルダン標準形と変換行列を求めるアルゴリズムにもなっている。
 
−
 
 
−
== 脚注 ==
 
−
{{reflist}}
 
−
 
 
−
== 参考文献 ==
 
−
* {{cite book
 
−
|和書
 
−
|last1    = 斎藤
 
−
|first1    = 正彦
 
−
|author    = 斎藤正彦
 
−
|year      = 1966
 
−
|title    = [http://www.utp.or.jp/bd/4-13-062001-0.html 線型代数入門]
 
−
|edition  = 初版
 
−
|publisher = 東京大学出版会
 
−
|isbn      = 978-4-13-062001-7
 
−
|ref      = harv
 
−
}}
 
−
* {{cite book
 
−
|editor    = Hogben, Leslie
 
−
|year      = 2007
 
−
|title    = Handbook of Linear Algebra
 
−
|url      = {{google books|n2g-x1OIbvYC|Handbook of Linear Algebra|plainurl=yes}}
 
−
|series    = Discrete mathematics and its applications
 
−
|publisher = Chapman & Hall/CRC
 
−
|isbn      = 978-1-58488-510-8
 
−
|ref      = {{sfnref|Hogben|2007}}
 
−
}}
 
−
 
 
−
== 関連項目 ==
 
−
* [[対角化]]
 
−
* [[スペクトル定理]]
 
−
 
 
−
{{Linear algebra}}
 
  
 
{{DEFAULTSORT:しよるたんひようしゆんけい}}
 
{{DEFAULTSORT:しよるたんひようしゆんけい}}

2019/4/27/ (土) 18:23時点における最新版

ジョルダン標準形（ジョルダンひょうじゅんけい、英: Jordan normal form）

逆行列の存在する行列を正則行列という。正方行列Aを正則行列Pを用いて変換する（P-1APを求める）とき、いちばん簡潔に求められる方法はフランスの数学者ジョルダンがみいだしたジョルダンの標準形である。たとえば三次正方行列は次のいずれかの形にかならず変換される。

00121081000100.gif

ただし、α、β、γはかならずしも相異なるとは限らない複素数（実数でもよい）である。

　一般的にいうと、まず、λを複素数（実数でもよい）とするとき、k次の行列J(λ, k)を

00121081000200.gif

により定義する。いくつかのJ(λ, k)の形の行列を対角形に並べた行列

00121081000300.gif

をジョルダン行列という。Aを正方行列とすればP-1APがジョルダン行列となる正則行列Pがかならず存在する。Aのジョルダン行列はAによって一意的に定まる。


楽天市場検索:



「http:///http:///mymemo.xyz/mymemo.xyz/wiki/index.php?title=ジョルダン標準形&oldid=275883」から取得